Proximal Operators¶
Definition¶
Let 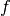 be a proper convex function mapping the normed space
be a proper convex function mapping the normed space 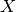 to the extended real number line
to the extended real number line ![(-\infty, +\infty]](../../../_images/math/5c255d9fe49273dfdb0b19df80e4103310bfd1cf.png) . The proximal
operators of the functional
. The proximal
operators of the functional 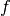 is mapping from
is mapping from 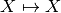 . It
is denoted as
. It
is denoted as ](../../../_images/math/72600e599429961f882bb1b2c46bd61e1b0a1069.png) with
with 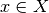 and defined by
and defined by
 = \arg\;\min_{y\in Y}\;f(y)+\frac{1}{2\tau} \|x-y\|_2^2](../../../_images/math/db6f4dff5d42d985a5de5eab0fcdbc350133f5b8.png)
The shorter notation 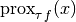 ) is also common.
) is also common.
Properties¶
Some properties which are useful to create or compose proximal operators:
Separable sum
If 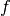 is separable across variables, i.e.
is separable across variables, i.e. 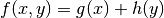 ,
then
,
then
 = (\mathrm{prox}_\tau[g](x), \mathrm{prox}_\tau[h](y))](../../../_images/math/0e8a3a5279a1bdc7a6f0a2ff458fa332a3af6c94.png)
Post-composition
If 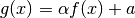 with
with 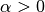 , then
, then
 = \mathrm{prox}_{\alpha\tau}[f](x)](../../../_images/math/80ba2baf50568b119d55dd98b055b711f4fb92ce.png)
Pre-composition
If 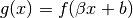 with
with 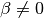 , then
, then
 = \frac{1}{\beta} (\mathrm{prox}_{\beta^2\tau}[f](\beta x+b)-b)](../../../_images/math/e9ef01685f9bcc28e52dab363617f7ec16a4eea5.png)
Moreau decomposition
This is also know as the Moreau identity
 + \frac{1}{\tau}\,\mathrm{prox}_{1/\tau}[f^*] (\frac{x}{\tau})](../../../_images/math/ee44ea605c0b0842646aea7da79d0828b9ddc25b.png)
where 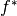 is the convex conjugate of
is the convex conjugate of 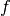 .
.
Convec conjugate
The convex conjugate of 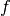 is defined as
is defined as
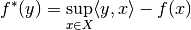
where 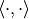 denotes inner product. For more
on convex conjugate and convex analysis see [Roc1970]
or Wikipedia.
denotes inner product. For more
on convex conjugate and convex analysis see [Roc1970]
or Wikipedia.
For more details on proximal operators including how to evaluate the proximal operator of a variety of functions see [PB2014].
Indicator function¶
Indicator functions are typically used to incorporate constraints. The
indicator function for a given set 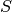 is defined as
is defined as
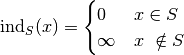
Special indicator functions
Indicator for a box centered at origin and with width 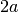 :
:
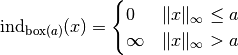
where 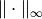 denotes the maximum-norm.
denotes the maximum-norm.