On the different notions of derivative¶
The concept of a derivative is one of the core concepts of mathematical analysis analysis, and it is essential whenever a linear approximation of a function in some point is required. Since the notion of derivative has different meanings in different contexts, this guide has been written to introduce the different derivative concepts used in ODL.
In short, different notions of derivatives that will be discussed here are:
- Derivative. When we write “derivative” in ODL code and documentation, we mean the derivative of an
Operator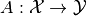 w.r.t to a disturbance in
w.r.t to a disturbance in 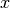 , i.e a linear approximation of
, i.e a linear approximation of 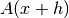 for small
for small 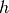 .
The derivative in a point
.
The derivative in a point 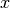 is an
is an Operator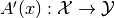 .
. - Gradient. If the operator
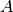 is a
is a functional, i.e.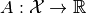 , then the gradient is the direction in which
, then the gradient is the direction in which 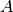 increases the most.
The gradient in a point
increases the most.
The gradient in a point 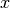 is a vector
is a vector ](../_images/math/cc8ca8899db17bf4665ffe92084280b206d983d5.png) in
in 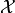 such that
such that , y \rangle](../_images/math/eac63291916904c770941441a9f2d3cddafd22cb.png) .
The gradient operator is the operator
.
The gradient operator is the operator ](../_images/math/89d4f56e710b7fe66b8fae6275bd76a7cf9f6949.png) .
. - Hessian. The hessian in a point
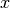 is the derivative operator of the gradient operator, i.e.
is the derivative operator of the gradient operator, i.e. ![H(x) = [\nabla A]'(x)](../_images/math/89d007fc38d555a0b2d1a84bb6c675ea187a1bd9.png) .
. - Spatial Gradient. The spatial gradient is only defined for spaces
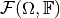 whose elements are functions over some domain
whose elements are functions over some domain 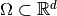 taking values in
taking values in 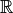 or
or 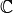 .
It can be seen as a vectorized version of the usual gradient, taken in each point in
.
It can be seen as a vectorized version of the usual gradient, taken in each point in 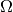 .
. - Subgradient. The subgradient extends the notion of derivative to any convex functional and is used in some optimization solvers where the objective function is not differentiable.
Derivative¶
The derivative is usually introduced for functions 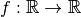 via the limit
via the limit
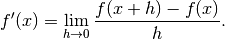
Here we say that the derivative of 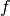 in
in 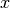 is
is 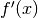 .
.
This limit makes sense in one dimension, but once we start considering functions in higher dimension we get into trouble.
Consider 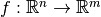 – what would
– what would 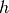 mean in this case?
An extension is the concept of a directional derivative.
The derivative of
mean in this case?
An extension is the concept of a directional derivative.
The derivative of 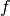 in
in 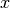 in direction
in direction 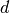 is
is 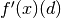 :
:
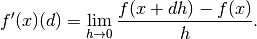
Here we see (as implied by the notation) that 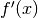 is actually an operator
is actually an operator
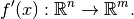
We can rewrite this using the explicit requirement that 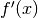 is a linear approximation of
is a linear approximation of 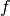 at
at 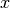 , i.e.
, i.e.
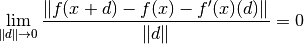
This notion naturally extends to an Operator 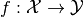 between Banach spaces
between Banach spaces 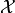 and
and 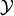 with norms
with norms 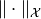 and
and 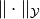 , respectively.
Here
, respectively.
Here 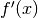 is defined as the linear operator (if it exists) that satisfies
is defined as the linear operator (if it exists) that satisfies
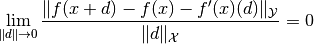
This definition of the derivative is called the Fréchet derivative.
The Gateaux derivative¶
The concept of directional derivative can also be extended to Banach spaces, giving the Gateaux derivative. The Gateaux derivative is more general than the Fréchet derivative, but is not always a linear operator. An example of a function that is Gateaux differentiable but not Fréchet differentiable is the absolute value function. For this reason, when we write “derivative” in ODL, we generally mean the Fréchet derivative, but in some cases the Gateaux derivative can be used via duck-typing.
Rules for the Fréchet derivative¶
Many of the usual rules for derivatives also hold for the Fréchet derivative, i.e.
Linearity
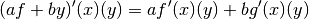
Chain rule
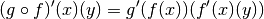
Linear operators are their own derivatives. If
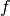 linear, then
linear, then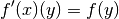
Implementations in ODL¶
- The derivative is implemented in ODL for
Operator‘s via theOperator.derivativemethod. - It can be numerically computed using the
NumericalDerivativeoperator. - Many of the operator arithmetic classes implement the usual rules for the Fréchet derivative, such as the chain rule, distributivity over addition etc.
Gradient¶
In the classical setting of functionals 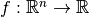 , the gradient is the vector
, the gradient is the vector
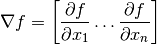
This can be generalized to the setting of functionals 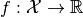 mapping elements in some Banach space
mapping elements in some Banach space 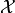 to the real numbers by noting that the Fréchet derivative can be written as
to the real numbers by noting that the Fréchet derivative can be written as
 \rangle,](../_images/math/8df413b141256dd6d0505c3095048943a00dec47.png)
where ](../_images/math/671043f3bfec6b8ccd5f66f7044fbf5afee6c284.png) lies in the dual space of
lies in the dual space of 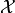 , denoted
, denoted 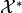 . For most spaces in ODL, the spaces are Hilbert spaces where
. For most spaces in ODL, the spaces are Hilbert spaces where 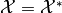 by the Riesz representation theorem and hence
by the Riesz representation theorem and hence 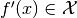 .
.
We call the (possibly nonlinear) operator ](../_images/math/39b242c33b9ad388f9247f5c3856159d8cef0bcf.png) the Gradient operator of
the Gradient operator of 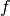 .
.
Implementations in ODL¶
- The gradient is implemented in ODL
Functional‘s via theFunctional.gradientmethod. - It can be numerically computed using the
NumericalGradientoperator.
Hessian¶
In the classical setting of functionals 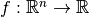 , the Hessian in a point
, the Hessian in a point 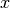 is the matrix
is the matrix 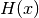 such that
such that
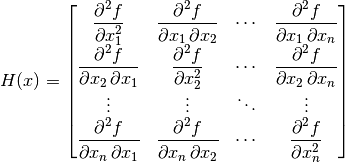
with the derivatives are evaluated in the point 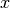 .
It has the property that that the quadratic variation of
.
It has the property that that the quadratic variation of 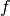 is
is
\rangle + \langle d, [H(x)](d)\rangle + o(\|d\|^2)](../_images/math/1e59bf0e50537d5f4cfa42b675ddb3bda0bf5b5d.png)
but also that the derivative of the gradient operator is
 + [H(x)](d) + o(\|d\|)](../_images/math/433b4026350743ac27b887fad15b517cbdbc403b.png)
If we take this second property as the definition of the Hessian, it can easily be generalized to the setting of functionals 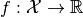 mapping elements in some Hilbert space
mapping elements in some Hilbert space 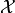 to the real numbers.
to the real numbers.
Implementations in ODL¶
The Hessian is not explicitly implemented anywhere in ODL. Instead it can be used in the form of the derivative of the gradient operator. This is however not implemented for all functionals.
- For an example of a functional whose gradient has a derivative, see
RosenbrockFunctional. - It can be computed by taking the
NumericalDerivativeof the gradient, which can in turn be computed using theNumericalGradient.
Spatial Gradient¶
The spatial gradient of a function 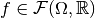 is an element in the function space
is an element in the function space 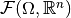 such that for any
such that for any 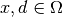 .
.
Implementations in ODL¶
- The spatial gradient is implemented in ODL in the
Gradientoperator. - Several related operators such as the
PartialDerivativeandLaplacianare also available.
Subgradient¶
The Subgradient (also subderivative or subdifferential) of a convex function 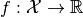 , mapping a Banach space
, mapping a Banach space 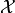 to
to 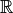 , is defined as the set-valued function
, is defined as the set-valued function 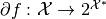 whose values are:
whose values are:
 = \{c \in \mathcal{X}^* \ s.t. \ f(x) - f(x_0) \geq \langle c , x - x_0 \rangle \forall x \in \mathcal{X} \}](../_images/math/30d40ec96cd5ba67c988e6c6b3f076f1f1d93ef1.png)
for functions that are differentiable in the usual sense, this reduces to the usual gradient.
Implementations in ODL¶
The subgradient is not explicitly implemented in odl, but is implicitly used in the proximal operators. See Proximal Operators for more information.