Glossary¶

array-like

Any data structure which can be converted into a numpy.ndarray by the numpy.array constructor. Includes all NtuplesBaseVector based classes.

convex conjugate

The convex conjugate (also called Fenchel conjugate) is an important tool in convex optimization. For a functional 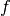$f$ , the convex conjugate 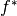$f^*$ is the functional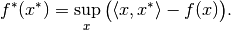

$f^*(x^*) = \sup_x \big( \langle x, x^* \rangle - f(x) \big).$

discretization

Structure to handle the mapping between abstract objects (e.g. functions) and concrete, finite realizations. It encompasses an abstract Set, a finite data container (NtuplesBaseVector in general) and the mappings between them, sampling and interpolation.

domain

Set of elements to which an operator can be applied.

dtype

Short for data type, indicates the way data is represented internally. For example float32 means 32-bit floating point numbers. See numpy dtype for more details.

element

Saying that x is an element of a given Set my_set means that x in my_set evaluates to True. The term is typically used as “element of <set>” or “<set>” element. When referring to a LinearSpace like, e.g., DiscreteLp, an element is of the corresponding type LinearSpaceElement, i.e. DiscreteLpElement in the above example. Elements of a set can be created by the Set.element method.

element-like

Any data structure which can be converted into an element of a Set by the Set.element method. For example, an rn(3) element-like is any array-like object with 3 real entries.

Example: `DiscreteLp` element-like means that DiscreteLp.element can create a DiscreteLpElement from the input.

in-place evaluation

Operator evaluation method which uses an existing data container to store the result. Usually more efficient than out-of-place evaluation since no new memory is allocated and no data is copied.

interpolation

Operator in a discretization mapping a concrete (finite-dimensional) object to an abstract (infinite-dimensional) one. Example: LinearInterpolation.

meshgrid

Tuple of arrays defining a tensor grid by all possible combinations of entries, one from each array. In 2 dimensions, for example, the arrays [1, 2] and [-1, 0, 1] define the grid points (1, -1), (1, 0), (1, 1), (2, -1), (2, 0), (2, 1).

operator

Mathematical notion for a mapping between arbitrary vector spaces. This includes the important special case of an operator taking a (discretized) function as an input and returning another function. For example, the Fourier Transform maps a function to its transformed version. Operators of this type are the most prominent use case in ODL. See the in-depth guide on operators for details on their implementation.

order

Ordering of the axes in a multi-dimensional array with linear (one-dimensional) storage. For C ordering ('C'), the last axis has smallest stride (varies fastest), and the first axis has largest stride (varies slowest). Fortran ordering ('F') is the exact opposite.

out-of-place evaluation

Operator evaluation method which creates a new data container to store the result. Usually less efficient than in-place evaluation since new memory is allocated and data needs to be copied.

proximal

Given a proper convex functional 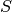$S$ , the proximal operator is defined by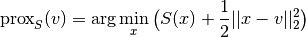

$\text{prox}_S(v) = \arg\min_x \big( S(x) + \frac{1}{2}||x - v||_2^2 \big)$

The term “proximal” is also occasionally used instead of ProxImaL, then refering to the proximal modelling language for the solution of convex optimization problems.

proximal factory

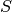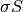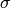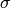A proximal factory associated with a functional $S$ is a callable, which returns the proximal of the scaled functional $\sigma S$ when called with a scalar $\sigma$ . This is used due to the fact that optimization methods often use $\text{prox}_{\sigma S}$ for varying $\sigma$ .

range

Set of elements to which an operator maps, i.e. in which the result of an operator evaluation lies.

sampling

Operator in a discretization mapping an abstract (infinite-dimensional) object to a concrete (finite-dimensional) one. Example: PointCollocation.

vectorization

Ability of a function to be evaluated on a grid in a single call rather than looping over the grid points. Vectorized evaluation gives a huge performance boost compared to Python loops (at least if there is no JIT) since loops are implemented in optimized C code.

The vectorization concept in ODL differs slightly from the one in NumPy in that arguments have to be passed as a single tuple rather than a number of (positional) arguments. See numpy vectorization for more details.